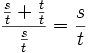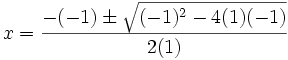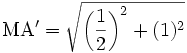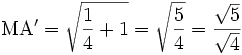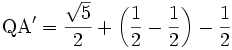Construct a pentagon/proof
I say the figure ABCDE is a regular pentagon.
Contents
Proof: Inscribed Pentagon
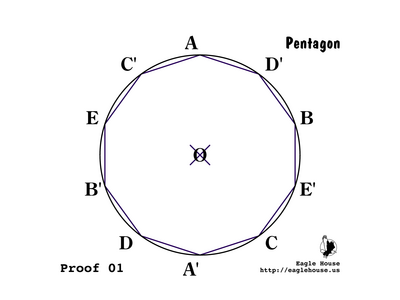
P 01
Consider a regular decagon AD'BE'CA'DB'EC' inscribed in a circle O with radius AO. Set AO = r = 1.
• We may consider the inscribed decagon given without having a construction.
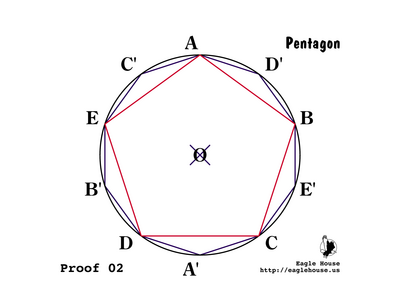
P 02
A decagon has 10 vertices and a pentagon has 5 vertices, so if we can construct the first then we can construct the second.
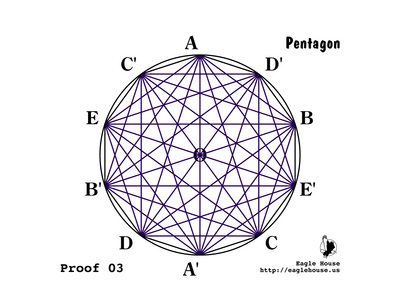
P 03
Connect every vertex of the decagon to every other vertex.
• This is called a complete graph.
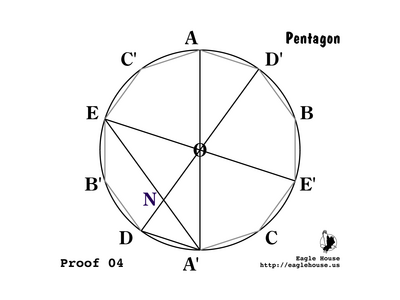
P 04
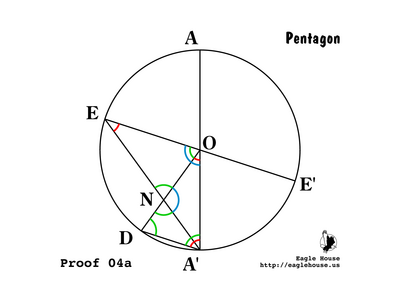
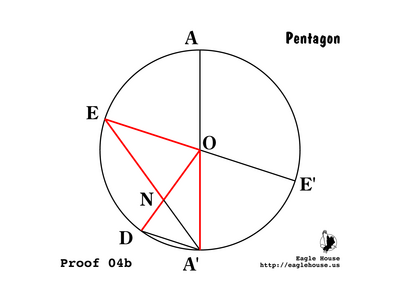
Remove most of the lines from the last figure, for simplicity. Find the intersection of DD' and A'E; call this N.
P 05
Since the complete circle has an angle of 2π, the angle connecting adjacent vertices (such as ∠A'OD) must be 2π / 10 = π / 5. Call this θ ("theta").
• We discuss angles in radians. The angle θ = π / 5 radians = 36°.
P 06
Since A'O and DO are both radii of circle O they are equal and triangle A'OD must be isosceles in O.
P 07
Since the sum of all angles in every triangle is π = 5θ and ∠A'OD = π / 5 = θ, ∠DA'O = ∠A'DO = 2π / 5 = 2θ.
P 08
• Equal angles inscribed in a circle subtend equal chords.
Arc AE = Arc ED, so ∠AA'E = ∠EA'D = (∠DA'O) / 2 = θ.
P 09
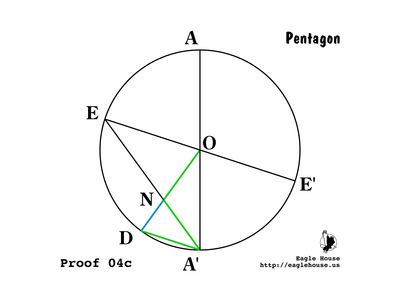
Since ∠EA'D = ∠NA'D = θ and ∠A'DN = ∠A'DO = 2θ, ∠A'ND = 2θ and so triangle A'DN is isosceles in A'; and A'N = DA'.
P 10
Since ∠NA'D = ∠A'OD, ∠A'DN = ∠A'DO, and ∠A'ND = ∠DA'O; therefore triangles A'OD and A'DN are similar (AAA) and the ratios of corresponding sides are equal.
So DO / A'N = DA' / ND = A'O / DA'.
Also DO / DA' = A'O / DA' = NA' / ND = DA' / ND.
P 11
Since ∠NA'D = θ and ∠DA'O = 2θ, ∠NA'O = θ. Thus triangle ONA' is isosceles in N; and A'N = NO. Also ∠A'NO = 3θ. By (P 09), A'N = DA' = NO; call this length g.
P 12
By (P 01), DO = 1. By (P 10) and (P 11), DO / A'N = DO / NO = 1 / g.
Also DO / NO = DO / DA' = NA' / ND = NO / ND = 1 / g.
Summary
The conclusions of (P 05) through (P 12) and later (P 16) are summarized in the figures above. The angles are θ, 2θ, and 3θ. The line lengths are 1, g, and 1 - g.
P 13
By (P 12), DO / NO = NO / ND. But DO = NO + ND. So by substitution:
- {EQ 01}
For convenience, let's rewrite this as:
- {EQ 02}
Call this ratio s / t = ![]() ("phi").
("phi").
P 14
Divide numerator and denominator of the left side by t:
- {EQ 03}
- {EQ 04}
- {EQ 05}
P 15
This is a quadratic equation, so put in standard form:
|
|
So a = 1, b = -1, and c = -1; using the quadratic formula:
|
|
Simplify to:
- {EQ 10}
The ratio NO / ND is positive, so we prefer the positive root:
- {EQ 11}
P 16
Since A'O = EO, triangle EOA' is isosceles in O. By (P 11), ∠NA'O = ∠EA'O = ∠OEA' = θ. Again, since the sum of angles in a triangle must be π = 5θ, ∠A'OE = 3θ. Therefore triangles A'OE and ONA' are similar (AAA); A'O / EA' = NA' / EO and A'O / NA' = EA' / EO.
P 17
By (P 09, 11, 12), the ratio A'O / NA' = 1 / g = ![]() ; by (P 16) this is also equal to EA' / EO. But since EO = 1, the length EA' is itself
; by (P 16) this is also equal to EA' / EO. But since EO = 1, the length EA' is itself ![]() .
.
P 18
We have already found (P 11) that the length DA' = g. By (P 13) we set 1/g = ![]() , so g = 1/
, so g = 1/![]() .
.
P 19
In (P 14) we found:
- {EQ 04}
Simplify:
Therefore:
- {EQ 15}
P 20
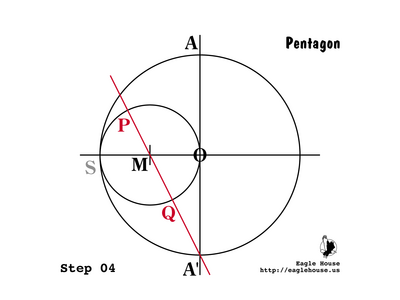
Now it is time to look again at our construction:
Since A'O = 1 and MO = 1 / 2, then by Pythagoras:
- {EQ 16}
Simplify:
P 21
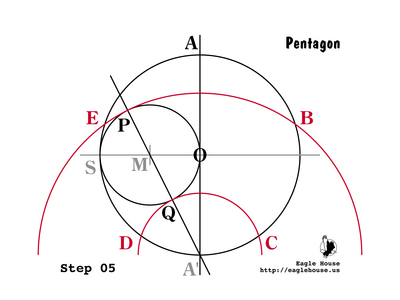
Since the radius of circle M is 1 / 2 (Step 2, 3), then OM = PM = QM = 1 / 2.
P 22
Since PA' = MA' + PM, then by (P 20, 21):
- {EQ 19}
which by (P 15) is also equal to ![]() . In (Step 5) we found E such that EA' = PA'. By (P 17), E and A' are indeed vertices of a regular decagon.
. In (Step 5) we found E such that EA' = PA'. By (P 17), E and A' are indeed vertices of a regular decagon.
P 23
Similarly, QA' = MA' - QM, so:
- {EQ 20}
Adding zero is of course allowed:
- {EQ 21}
Regroup:
which is equal to ![]() - 1 (P 15). In (Step 5) we found D such that DA' = QA'. By (P 17), D and A' are indeed vertices of a regular decagon.
- 1 (P 15). In (Step 5) we found D such that DA' = QA'. By (P 17), D and A' are indeed vertices of a regular decagon.
P 24
By similar arguments we show that B and C are also vertices of a regular decagon. Since a decagon has an even number of vertices, A is also a vertex. And by (P 02), we have also found the vertices of a regular pentagon. QED.